$\LaTeX$ Workshop

These were written to accompany a GBM tutorial by Mike Wahl and Dan Waxman, but hopefully should be a decent reference in the future regardless. We'll also embed a recording of the meeting later. There's a corresponding document here, but most examples can be edited from this webpage directly. This differs a bit from the actual presentaton and the corresponding document due to some limitations, but is mostly the same.

What is $\LaTeX$?

$\LaTeX$ (pronounced to rhyme with "tech") is a markup language, similar in theory to HTML/CSS. Just as the internet is built upon HTML/CSS, high-quality typeset papers in math and physics are often built upon $\LaTeX$. It builds upon $\TeX$, built by Don Knuth in the late 70s and 80s, after getting annoyed with the typesetting issues writing the first few volumes of The Art of Computer Programming.

Somewhat confusingly, we type out our documents in $\LaTeX$, then pass it to a program named something similar like pdfTeX, which converts our markup into a pretty, readable format. In physics classes, most people end up using $\LaTeX$ for professional-looking lab reports, but people also make beautiful lecture notes and awesome resumes.

Why do we use it?

Simply put, it makes life easier. Juxtaposed to many word processors, $\LaTeX$ just works; after learning what you should type, it's not very often you have to change anything for it to render nicely, it's already nice. Instead of taking ten minutes to type the wave equation, it takes ten seconds and looks great. In order to render \[\nabla^2 f = \frac{1}{c^2} \frac{\partial^2 f}{\partial t^2},\] we just need to type \[\tt{\backslash nabla\verb!^! 2\, f = \backslash frac\{1\}\{c\verb!^!2\} \backslash frac\{\backslash partial\verb!^!2 \, f\}\{\backslash partial \, t\verb!^!2\}}.\]

Packages

One of the most miraculous aspects of $\LaTeX$ is the community surrounding it. While some things are somewhat cumbersome in straight-up $\LaTeX$, we can use some other people's code to make our lives easier with packages.

At the top of the reference document, you'll see a number of packages being used. Things like graphicx make inserting figures easy, while other packages like siunitx help make the process of writing out units much easier.

General Navigation

Like anything else, there's some general structure to $\LaTeX$ documents: we put stuff about how we want our document to look in the preamble, then the rest of our code in the body. There's also math mode and text mode; in text mode you type normally, but in math mode, which you access by typing $stuff here$ , you can type math expressions like we'll see below.

In $\LaTeX$, there's also environments, which we'll explore later as well.

Equations

Finally, the place where $\LaTeX$ shines. It shines so bright that when Microsoft was looking to make writing equations easier, they implemented many of the basic $\LaTeX$ commands. To help out here, we've made it so you can edit stuff in here and see the results live. Feel free to edit any of the examples below and see the results!

We'll start off with some integrals, which you'll end up typing a lot in physics. Everything starts with the wonderful \int command, which creates the familiar looking S. We can add limits of integration (or in fact, general sub- and super-scripts) using the caret ^ and underscore _.

\[S = \int_{t_0}^{t_1} S(q, \dot{q}, t) \, dt.\]

There's a few little useful tricks in the last example which are worth exploring. For one, it's not too hard to see that writing \int_t_0^t_1 would be terrible ambiguous, which computers hate. So when you want to group things together in $\LaTeX$, you can just slap on some curly braces.

For spacing purposes, we added \, before the differential $dt$ as well --- you can play around with this above to see what the difference looks like.

Another thing we used is the Newtonian notation for derivative, \dot{q}. If we wanted, say, the second derivative, we could use \ddot{q} instead. So Newton's Second Law would look like

\[\vec{F} = m\ddot{q}.\]

(Here, we found another useful little symbol: \vec{v}.)

While on the topic of symbols, Greek letters are everywhere in physics. For Greek letters, you can use \letter for the lowercase and \Letter for uppercase in math mode. The only exception is when letters are the same in Greek and English, so things like \Alpha don't mean anything. In this example, we'll also see fractions for the first time, where the syntax is just \frac{numerator}{denominator}.

\[\int_0^\infty \frac{x^{s-1}}{e^x - 1} \, dx = \Gamma(s) \zeta(s).\]

Obviously, typesetting homework is nice; if nothing else it makes your work easier to read for the TA. But here you'll have to show your work! You can do this sort of thing with the align environment.

\[\begin{align} U_0 &= 2 \sum_{n \leq n_F} \epsilon_n \\ &= \pi \int_0^{n_F}dn\, n^2 \epsilon_n \\ &= \frac{\pi^3}{2m} \left(\frac{\hbar}{L}\right)^2 \int_0^{n_F} dn\, n^4. \end{align}\]

Figures

Unfortunately, it's not really possible to make this editable in a website. Instead, we recommend you check out the accompanying file in Overleaf and play around there. Some notes are provided for completeness.

Figures are nothing new, and unfortunately LaTeX can complicate what is otherwise a simple matter of placing a picture on the page. First off, we must add the graphicx package, which will let us use outside images. Next, we need to specify our graphics path with \graphicspath{}. To keep things tidy, we've created two folders in overleaf, one labeled images and the other plots, hence why our statement includes both of them: \graphicspath{{./images/} {./plots/}} . When including a picture, it is best practice to place it inside the figure environment, and this is where the funky business can begin.

$\LaTeX$ floats are weird. They're intended to make figures and tables as unobtrusive as possible, but they have a habit of ignoring where you want them to go. Default LaTeX includes the [h] parameter to specify "here", but in practice, it is best to use [H] from the float package.

\begin{figure}
    \centering
    \includegraphics{Intro Full Adder}
    \caption{Keep reading, ignore for now}
    \label{fig:FA}
\end{figure}

\begin{figure}[H]
    \centering
    \includegraphics[width=10cm]{loc}
    \caption{Notice how this appears in the place you'd expect it to: below the paragraph in the code. The other figure wanders off seemingly without reason.}
    \label{fig:location}
\end{figure}

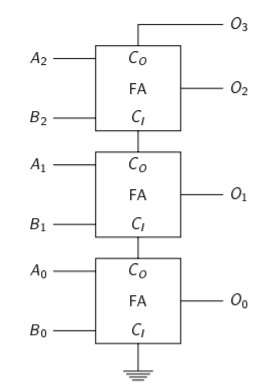
There are other letters which can go in place of [H] and have different effects, but those are rarely useful. If you need to use them, Google is your friend. Also of note is image sizes. You'll frequently run into errors where you'll need to resize the image to fit it on the page. This can be done several ways, but mainly with the [width= x cm] option. Finally, you may be wondering what the \label{} statement means. This lets us reference certain figures and tables without worrying about if our future edits to the document change the order or page where the given figure appears. For example, to reference the table we saw earlier, we can write the following: see Table~\ref{tab:IV} on page~\pageref{tab:IV} for more information. It also lets us list all of the tables or figures with a single command, should we need it in an appendix or such.

Tables are somewhat annoying, but there are tools to help us out. In the talk, Mike talks about a Google Sheets add-on LatexKit, which should be useful for you in your labs.

Macros

There's a package for almost everything, but nonetheless it's often convenient to define some macros. For example, typing \mathbb{R} for the real numbers $\mathbb{R}$ can get really cumbersome really quickly. But defining a macro so that we just need to type \R is way less typing.

The way we do this is by specifying commands in our preamble. For example, if we'd want to use \R as shorthand for \mathbb{R}, we would write \newcommand{\R}{\mathbb{R}}.

\[\newcommand{\R}{\mathbb{R}} \int_\R \exp(-x^2) \, dx = \sqrt{\pi}.\]

This is a super useful macro, and usually one of the first people use, but also kind of trivial. We can also look at some slightly more complicated behavior, like writing down partial derivatives. We can use the cool package to get nice and convenient partial derivatives, but as an exercise let's develop a macro for it now.

For this, we're going to now need arguments in our macro; namely, we're going to create an optional argument for the numerator, an a required argument for the denominator. We won't worry about higher order partials right now, but again check out the aforementioned package for mixed partials and smart spacing.

\[\newcommand{\pder}[2][]{\frac{\partial#1}{\partial#2}} % https://tex.stackexchange.com/questions/29179/partial-derivative-macro \newcommand{\der}[2][]{\frac{\mathrm{d}#1}{\mathrm{d}#2}} \begin{cases} \pder[H]{q} = -\der[p]{t} \\ \pder[H]{p} = \der[q]{t} \end{cases}.\]

On top of all this, we can also override commands usiing \renewcommand. For example, it's common to type out vectors as $\mathbf{v}$ instead of $\vec{v}$. We can then override \vec so that, with one line, all of our vectors are changed.

\[\renewcommand{\vec}[1]{\mathbf{#1}} \int_\gamma \vec{F} \, d\vec{r} = \iint_S (\nabla \times \vec{F}) \cdot d\vec{S}.\]

Beyond this, we won't have a ton of time for a one hour workshop, but you can find a more complete reference here.

Document Settings

Very few documents actually look like the default article class in LaTeX. But in the header we can specify some changes to get the pages how we want to look. Also, use a template. Maybe I'll make one available and link it here. For this, the geometry package is a useful tool though.

Concluding Remarks

$\LaTeX$ rules, Microsoft Word drools.

\(\LaTeX\) Workshop

What is \(\LaTeX\)?